A Case Study on Stellar Evolution of Single and Binary Stars

Abstract

Stars are a gigantic sphere of gases burning to produce and emit light. These burning balls are one of the most common celestial objects in space and they travel around the galaxy, being massive they have strong gravitational pull; therefore, it might happen that a massive star captures another passing star, and it may create a new binary pair. It is to be noted that when one looks at the night sky many points are twinkling intense bright light, which in fact might be that the single twin-kling point are two stars orbiting one another. The cosmos is humungous, ever-growing, and continuously expanding. It houses all celestial and unknown objects full of mystery. It includes planets like earth hosting life, the asteroids, and mete-ors, to the energy source of the infinite universe the stars and the phenomenon who hasn\\\'t been able to be captured clearly by man and is still a mystery, the black holes and the list goes on and on. From time unknown, mankind has been fascinated by cosmos and its endless possibilities. In this research paper, stellar evolution of single and eclipsing binary stars to get more insight into has been discussed.

Introduction

I. INTRODUCTION

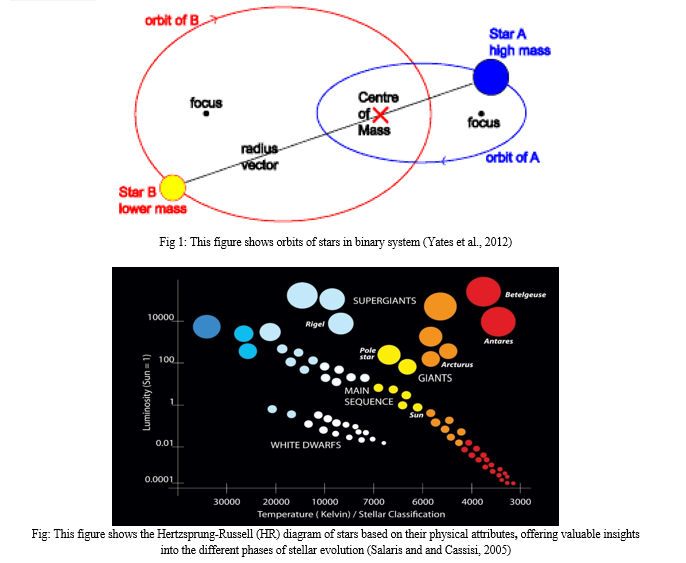
Stars and their evolution have been important research from decades to understand the universe, its existence, nature and to study the nature and formation of planets (Bertone et al., 2007; Asplund et al., 2009; Collision et al., 2013; Huang et al., 2019; Laplace et al., 2022;). There are several stages of any star’s evolution (Hawken and Bridle, 2009). Stellar evaluation or the evolutionary track of a star tells us about the formation of a star with its initial changes and processes comprising chemical reactions involved, and how the star undergoes transformation at its near end life and after its death (Ellison et al., 2007). Till today's date about 88% of stars are a part of binary systems and some of them being a part of a high order system (Dave et al., 2011). Fig 1 shows the physical mechanism of the formation of a binary star. Mass of a star is a significant component which provides information how a star evolves during its whole lifetime and what the fate holds for the star in the formation of any stars which was initiated in a Nebula.  (Kroupa, 2001). As high mass stars have lower lifetime as compared to stars with lower mass due to amount of fusion reaction occurring and the amount of energy it creates in its main sequence phase (Eliiison et al., 2007). It is known from recent studies that stellar gases are massive clouds composed of materials like dust, gas in the form of hydrogen and helium and plasma in the interstellar medium (Lagos et al., 2011). In addition to the gases, dust particles present in the stellar cloud have a wavelength of about 2540Å and even in this dimension the dust particles are effective in scattering the light of distant stars and thereby rendering our visibility to get a clear idea (Laplace, 2022). Therefore, nebula formation occurs when a considerable amount of interstellar medium is acted upon by gravity and undergoes gravitational collapse due to which the all the matter gets accumulated to form clumps forming regions around interstellar medium with higher densities (Mannucci et al., 2010). However, the density of these stellar gas clouds is very less due to its abundance and the enormous size of galaxy (Nagao et al., 2006). Depending on the size and amount of stellar gas cloud, it can consist of up to 1/10 of the total mass of a galaxy and this much amount of stellar gas clouds can support the formation of stars (Kroupa et al., 2001). In the initial phase of the star formation, ‘dark globules’ are formed due to the influence of gravity in the gas cloud. Further, due to formation of denser regions, a protostar is formed and due to influence of gravity, it undergoes contraction. In this process, about one half of the protostars’ stored potential energy gets converted in the form of heat, that increases the protostar’s central temperature, and the remaining portions energy is just radioed in the interstellar medium Pinzke, and Pfrommer, 2010). As the protostar is undergoing contraction it would not forever be under the process of contraction, but as the temperature rises and when this temperature reaches a certain temperature limit also known as the critical temperature, due to this energy generation starts in the interior of the protostar and this newly generated energy compensates for the energy being radiated away from the surface now we can observe a state of equilibrium, beyond which there is no further contraction and a gigantic sphere is obtained with the star’s core temperature about 15 Million K now according to the mass of the protostar and the main sequence star (Mannucci et al., 2010). It was further suggested that as the star enters its main sequence the stars remain here for a long time and this stage of the total lifespan of star covers 80-90 % of its life (Salaris et al., 2005; Nagao et al., 2006). In different stages of star’s life, various kinds of chemical cycles occur inside the star such as the PP cycle, CNO cycle, He fusion etc (Swinbank et al., 2009).

II. CHARACTERISTICS OF STARS

A. Physical Parameters of Stars

Mass, Luminosity and Radius of any star are reared as the fundamentals parameters of star affecting its evolution (Salaris et al., 2005; Pinzke and Pfrommer, 2010). All these parameters were observed to be time dependent and change during time. Besides these three parameters, various parameters like the angular momentum, magnetic field, the mass loss rate of star and pulsation period become important regarding stellar evolution (Swinbank et al., 2009). The stars’ luminosity is nearly proportional to the cube of its mass (Asplund et al., 2009). Main            sequence stars are found to be more massive than this relative to their luminosity. They would be in danger of collapsing under their own gravitational force. Less massive stars would be blown apart by radiation pressure from the intense luminosity (Dave et al., 2011).

B. Description of Hertzsprung-Russel (HR) Diagram

The HR diagram is a powerful tool which is used to study and track the star’s evolution (Fig 2). Onn the x axis of the graph we take temperature which increases from right to left along the x axis and on the y axis we can take the luminosity of the star. We can also take other parameters in y axis such as the spectral color of stars. Absolute Magnitude is plotted against these axes too. The placement of stars in the HR diagram tells ample amount of information one needs to get for any stars as the whole diagram is divided into segments based on various stage of star’s life, its mass, Luminosity and so on (Swinbank et al., 2009; Huang et al., 2019). The most prominent line or the area on the HR diagram is the almost straight diagonal line which runs from the top left of the diagram to bottom right which is referred as the main sequence line. In this region roughly about 90% of the stars are located, as the main sequence is the most dominant and longest time in any star’s evolutionary track. Stars have been further classified based on temperature as spectral orders of O, B, A, F, G, K, and M, starting from hottest to closest and then each class is further divided into 0- 9 based on temperature (Kroupa, 2001). Colors have been assigned to these classes. One can also obtain the luminosity of star by using the Stefan Boltzmann law (L = 4πR2 σT4) following Nagao et al., (2006). In the formula, the term ‘L’ is designated to the luminosity, R being the star’s radius, and the term ’T’ represents the temperature of star and σ is Stefan’s constant. Using it, one can see that if we take 2 stars one both above the main sequence line with higher luminosity and having similar température comparing to the cooler main sequence stars are found to have a larger surface area implying that they also possess larger radius too. One can also conclude that any bright and cool star must be extremely humungous in size and that stars that are hot yet dim have comparable small surface area. Red giants are an enormous state of star after its main sequence which occurs when the star can’t sustain anymore Hydrogen thermal fusion thus starts to fuse other heavy elements. These gigantic stars are placed right above the main sequence diagonal line. White Dwarfs are placed below the main  diagonal sequence line (Mannucci et al., 2010).

C. Instability region in HR diagram

It is to be noted that that there are many stages in a life of a star’s evolution (Hawken and  Bridle, 2009). Moreover, there can be scenarios when the so-called life stage track in their evolution is not under equilibrium. These insatiable stars seem to pulsate. These stars quiver, and their action can be described as a human lung dilating and shrinking in size (Laplace, 2022). Under normal circumstances, when the star forms and starts to generate and emits its own light and energy, the forces of gravity and thermal pressure of star counteract each other (Nagao et al., 2006). For the stability of any general star, thermal pressure and the gravitational force must balance each other. The phenomenon of instability arises in the first instance when the above said forces are battling against each other (Salaris et al., 2005). A region in the HR diagram of a star is for the condition called as Instability Strip. The strip covers an area   approximately 1000 Kelvin (Swinbank et al., 2009). A type of stars which pulsates, meaning both their temperature and diameter varies and these parameters are known as the Cepheid Variables. They are considered as a valuable segment of this state. Their Luminosity is variable to the pulsation of these stars (Yin et al., 2007). On the HR diagram, they are placed at the top of Instability Strip. Some of the remarkable stars of this strip are W Virginis, RR Lyrae Stars both located at top and bottom of the diagram in the strip (Kroupa et al., 2001).

D. Metallicity of Star

Moreover, the metallicity of a star is also a significant criterion for stellar evolution (Wittkowski et al., 2005). Metallicity is basically the riches of elements existing in the universe that have more atomic weight than the elements Hydrogen and Helium which are the most abundant visible and detectable matter in the universe (Laplace, 2022).  Metallicity measures the abundance of the elements heavier than hydrogen and helium such as carbon, oxygen, iron, and others (Yates et al., 2012). In stellar astrophysics, it usually signifies the abundance of iron and is defined as the iron-to-hydrogen ratio (Kroupa et al., 2001).

It was found that stars, which have higher metallicity than the Sun are more probable to support planets as compared to the stars having lower metallicity (Yates et al., 2012). More recent studies support that the metallicity of any star has direct influence on its luminosity, mass, and velocities etc (Yin et al., 2007). Galaxies can have different amounts of mass of interstellar gas clouds (Mannucci et al., 2010). The lower mass galaxies can be visualized as having a comparably high interstellar gas ratio star mass which in short indicated the richness of metallic quantity that happened to be low (Nagao et al., 2006). It was found that if the size of the galaxy changes by a factor of two, the metallicity of the galaxy can change by 0.1 decimals (Huang et al., 2009; Yates et al., 2012). In this paper, we shall discuss the evolution stages of single stars and the characteristic properties of eclipsing binary stars.

III. ECLIPSING BINARY STARS

When one looks at the night sky, many points are twinkling light which in fact might be that the single twinkling point are two stars orbiting one another. Some of them being a part of a high order system. An example of binary system is Sirius. Binary stars can be classified into the following types based on their visuality (Salaris et al., 2005).

1. Visual Binaries: An individual can spot the pair star using telescope. Only about 5 to 10 percent of visible stars are visual binaries. One must note that it is not possible to view binary stars with the naked eyes.
2. Spectroscopie Binaries: They appear close even when telescope is used to view or study them
3. Eclipsing Binaries: These are the two stars of system have an orbit at angle such that when viewed w.r.t Earth, as one passes before other star making it look like an eclipse.
4. Astrometric Binaries: In this system the stars looks as if they are dancing in an empty space.

It is from this system that empirical mass-luminosity relationship (MLR) can be obtained which is useful in finding the masses of single stars being minority in universe.

Also, after getting the luminosity dip, the next easiest parameter to obtain is the time period, which can be done as follows:

First, we note the start day of orbit and the last day of orbit in the flux plot/

Then we observe the highest dip and how frequent it has been occurring.

TIME PERIOD = (END DAY - START DAY)/ frequency of highest dip between start and end day
Top width time lapse(A-D) = the phase*time period 

Bottom width time lapse (B-C)= the phase*time period

By taking the average of these two, we can find the time lapse of the eclipse.

The velocity of the stars can be found by obtaining the spectra of each star during its entire course of motion using Doppler shift.

The radius of stars can be found using the following formula.

Radius   = 0.25 * [ (A - D) + (B - C) ] * (v1 + v2)

It gives us radius for one of the stars in binary system here in this example it is for star 1

The mass of the binary star can be calculated by applying the corrected Kepler law of motion given as follows.

P2 = 4*(3.14)2/G (m1 + m2 )*a3

Where P is the period of orbit, G is Universal Constant of Gravitation, m1 and m2 are the masses of the stars and a is the radius of semi-major axis. It is to be noted that in a binary star, the semi-major axis is just the sum of the radius of the two stars.

A. Evolutionary Stages of Binary Stars

Now talking about two binary stars altering their evolution, as one moves farther from one another, gravity change is observed, thereby the force exerted by gravity shifts (Wittkowski, 2005). In this process, the gas which is far from the center of the first star may face a situation where the gas is pulled onto the next star in the system. This region in which the second star can pull the gas in is deemed the Roche Lobe. When a new system of binary is born, both might be well within the Roche Lobes. The case differs when the star which has higher mass between the two stars evolves faster into the red giant phase. In this phase, the star’s radius increases to an extent that it fills up its own Roche Lobe and as it expands in its size, material that is in the outermost layer of this red giant escapes the Roche Lobe and gets pulled to its other companion star in the system (Yin et al., 2007). We know now that the binary stars revolve around their center of mass. When they are in motion, the mass is changed, and the fixed angular momentum is conserved during this exchange. Now there can be two cases as to where the mass is getting transferred.

Case 1: If mass which is being exchanged moves from the star of lower mass to the higher mass star to conserve angular momentum, the lower mass star must move farther from the system’s center of mass and the distance between them must increase.

Case 2: If mass which is getting exchanged goes from a higher mass star to the lower to conserve angular momentum, the star with lower mass should be pulled closer to center of mass, and the distance between them would decrease.

From the discussion of the above two cases, one can see that the transfer of mass affects the separation in binary system, and we can conclude that when the masses of the pair is equal, they are closest. Now since the first star has been transferring so much mass to other stars, the distance between them increases again thus further stopping the mass transfer. The second star now becomes more massive. The first star that has low mass is on the way to become either white dwarf, black hole, or neutron star, which depends on the mass of core of that star      (Swinbank et al., 2009). Also, there may be a chance that it may go supernova, if it occurs the binary may survive, which will lead to creation of exotic systems for example pulsars or black holes which will be orbiting the main-sequence star (Lagos et al., 2011).

IV. ACKNOWLEDGEMENT

The corresponding author is thankful to the different scientists of Indian Institute of Astrophysics, Bengaluru for their motivation to complete this work.

Conclusion

The mass of a star has a significant impact on its stellar evolution. More massive stars have shorter main sequence lifetimes and are more likely to end their lives in a supernova explosion. The mass of a star also affects its chances of merging with another star. More massive stars are more likely to merge, which can lead to the formation of even more massive stars. Stellar evolution codes are a valuable tool for understanding the evolution of stars and galaxies. It is important to be aware of the limitations of stellar evolution codes and to compare the results from different codes to get a more accurate picture of stellar evolution.

References

[1] Asplund, M., Grevesse, N., Sauval, A. J., and Scott, Pat, The Chemical Composition of the Sun, Annual Review of Astronomy and Astrophysics, Vol. 47(1), 2009, pp. 481-522. [2] Bertone, Lucia, G. De, and Thomas, Peter A., The recycling of gas and metals in galaxy formation: predictions of a dynamical feedback model, Monthly Notices of the Royal Astronomical Society, Vol. 379(3), 2007, pp. 1143–1154. [3] Collison, F. M. and Poe, Kevin, “Astronomical Tourism”: The Astronomy and Dark Sky Program at Bryce Canyon National Park, Tourism Management Per-spectives, Vol. 7, 2013, pp. 1-15. [4] Dave, R., Finlator, K., Oppenheimer, B. D., Galaxy evolution in cosmological simulations with outflows – II. Metallicities and gas fractions, Monthly Notices of the Royal Astronomical Society, Vol. 416, Issue 2, 2011, pp. 1354–1376. [5] Ellison, S. L., Patton, D. R., Simard, Luc, and McConnachie, Alan W., Clues to the Origin of the Mass-Metallicity Relation: Dependence on Star Formation Rate and Galaxy Size. The Astrophysical Journal, Vol. 672, Issue 2, 2007, pp. L107-110. [6] Huang, L., Adams, F. C. and Grohs, E. Sensitivity of carbon and oxygen yields to the triple-alpha resonance in massive stars, Astroparticle Physics, Vol. 105, February 2019, pp. 13-24. [7] Hawken, A. J. and Bridle, S. L., Gravitational flexion by elliptical dark matter haloes, 2009, 1132-1138. [8] Kroupa, P., On the variation of the initial mass function. Monthly Notices of the Royal Astronomical Society, Vol. 322, Issue 2, April 2001, pp. 231–246. [9] Lagos, C. del P., L, Lacey, C. G., Baugh, C. M., Bower, R. G. and Benson, A. J., On the impact of empirical and theoretical star formation laws on galaxy for-mation. Monthly Notices of the Royal Astronomical Society, Vol. 416, Issue 2, 2011, pp. 1566–1584. [10] Laplace, E. T., A Tool for Understanding the Lives, Interiors, and Physics of Stars, Astronomy and Computing, Vol. 38, January 2022, 100516. [11] Mannucci, F., Cresci, G., Maiolino, R., Marconi, A. and Gnerucci, A., A fundamental relation between mass, star formation rate and metallicity in local and high-redshift galaxies. Monthly Notices of the Royal Astronomical Society, Vol. 408, Issue 4, 2010, pp. 2115–2127. [12] Nagao, T., Maiolino R. and Marconi, A., Gas metallicity diagnostics in star-forming galaxies. Astronomy and Astrophysics, Vol. 459, 2006, pp. 85-101. [13] Pinzke, A. and Pfrommer, C., Simulating the ?-ray emission from galaxy clusters: a universal cosmic ray spectrum and spatial distribution, The Astrophysical Journal, Vol. 409, 1, 2010, pp. 449-480. [14] Salaris, Maurizio and Cassisi, Santi. Evolution of Stars and Stellar Populations, John Wiley, and Sons. 2005, pp. 119–121. [15] Swinbank, A. M., Webb, T, M., Richard, J., Bower, R. G., Ellis, R. S., Illingworth, G., Jones, T., Kriek, M., Smail, I., Stark, D. P. and Dokkum, P. V., A spatially resolved map of the kinematics, star formation and stellar mass assembly in a star-forming galaxy at z= 4.9, 2009, 1121-1131. [16] Wittkowski, M., Fundamental stellar parameters, Bulletin de la Soci ?e Royale des Sciences de Li`ege - Vol. 74, 1-2-3, 2005, pp. 165-181. [17] Yates, R. M., Kauffmann, G. and Guo, Qi, The relation between metallicity, stellar mass, and star formation in galaxies: an analysis of observational and model data, Monthly Notices of the Royal Astronomical Society, Vol. 422, 1, May 2012, pp. 215–231. [18] Yin, S. Y., Liang, Y. C., Hammer, F., Brinchmann, J., Zhang, B., Deng, L. C. and Flores, H., Empirical strong-line oxygen abundance calibrations from galaxies with electron-temperature measurements. Astronomy and Astrophysics, Vol. 462 (2), 2007, 535-546.

Copyright

Copyright © 2024 A Kumar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.